Batch 3 - Class 148 - Mathematical Treasure Hunt
Preclass Exercise:
(536Henry: Problem 297) Here is a square plot of land with four houses, four trees, a well (W) in the center, and hedges planted across the four gateways (G). Can you divide the ground so that each householder shall have an equal portion of land, one tree, one gateway, an equal length of hedge, and free access to the well without trespass?
.png)
- Answer:
.png)
Attendance: Muskaan, Anshi, Siddhant, Arnav, Anishka, Liza, Arjun, Zorawar, Damini
Class Notes:
Mathematical Treasure Hunt
The group is divided into two teams. Each team has ten problems to be solved one after the other. The teams can pick the order of solving the problems - each team chooses one problem, and can solve that. Once they solve that problem, they can pick another problem, and so on. At any point, the team can "park" a problem they are solving, and go to another problem. Team that solves any problem correctly first gets 10 points. An incorrect solution takes that problem out of the game for that team (zero points). If the team is second to solve a particular problem, they get 5 points.
The game continues till the game master wants (yeah!) - normally, to let both teams finish, but depends on time availability. Game master can also give consolation marks to teams for interesting attempts, even in failed questions.
Problems for today (Mathematical Circus, Chapter 15):
- With a 7 minute hourglass and a 11 minute hourglass, what is the quickest way to time the boiling of an egg for 15 minutes?
- A man traveled 5000 miles in a car with one spare tire. He rotated tires at intervals so that when the trip ended, each tire had been used the same distance. For how many miles was each tire used?
- A standard deck of 52 cards is shuffled and cut. The color of the top card is noted. This card is replaced on the top, and the deck is cut again. Once more the color of the top card is noted. What is the probability that the color of two cards is the same? Note that a cut means removing at least one card (you can't tap at the top).
- Find a number base other than 10, in which 121 is a perfect square.
- Draw six line segments of equal length to form eight equilateral triangles.
- Assuming that an angle can not be trisected by compass and ruler, prove that no number in the doubling series 1,2,4,8... is a multiple of 3.
- A farmer has 20 pigs, 40 cows and 60 horses. How many horses does he have if you call the cows horses?
- Interpret: "He spoke from 2222222222222 people."
- A greek was born on 7th day of 40 B.C. and died on seventh day of 40 A.D. How many years did he live?
- A woman either always answers truthfully, always lies, or alternates true and false answers. How, in two questions, each answered by yes or no, can you determine whether she is a truthteller, liar or an alternater?
- Personalities Quiz - 5 points per personality correct. If someone guesses incorrectly, they can't take a second guess.
Now once we know who has won, we get to the discussion of answers. Allow the team that won a particular question to explain and answer first:
- Answer: Start the 7 and 11 minute hourglass together, and drop the egg to boil simultaneously. When sand stops running on 7 minute, turn it over. When sand stops running on 11 minutes, turn the 7 minute hourglass again (it now has 4 minutes again to run). When the sand stops now in 7 minute hourglass, 15 minutes would have elapsed.
- Followup: What if we didn't want to minimize the time, but number of times we flip the hourglass? Start the 7 and 11 minute hourglasses. When the 7 minute hourglass runs out, drop the egg in to boil. When the 11 minute timer runs out, flip it over. Now when the 11 minute hourglass runs out again, the egg would have boiled for 15 minutes. Note that this requires only 1 flip.
- Each tire is used 4/5 of the time, and hence for 4000 miles.
- Regardless of which card you cut first, it cannot be the top of the second cut. So there are 25 out of 51 cards that are of the same color. Hence 25/51
- 121 is a perfect square in any base > 2. Quick proof is to observe that 11 x 11 in any base > 2 is 121. Students may verify for different bases - for example 121 in base 3 is 1+6+9=16. 121 in base 4 is 1+4+16=25, and so on. In fact, Craig Schensted showed that with suitable definition of "perfect squares", 121 is a square even in systems based on negative numbers (ask kids to check), fractions, irrational numbers and complex numbers.
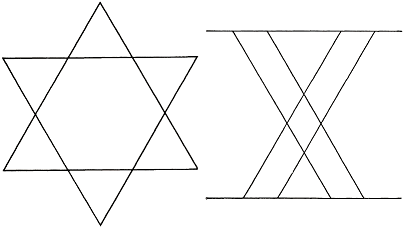
- Any angle can be bisected using a compass and ruler. So if any of the numbers 2,4,8,16 ... were a multiple of 3, we could successively bisect into those many equal parts, and hence be able to trisect the original angle. Proof by contradiction.
- The farmer has 60 horses. Calling a cow a horse doesn't make it a horse. (This joke is attributed to Abraham Lincoln - He once asked a man who had been arguing that slavery was not slavery but a form of protection, how many legs a dog would have if you called its tail a leg. The answer, said Lincoln, is four because calling a tail a leg does not make it a leg)
- "He spoke from 22 to 2 to 2:22 to 2,222 people" or "He spoke from 22 to 22 to 22:22 to 22 people"
- The greek lived 79 years. There is no 0 year.
- Ask the woman "Are you an alternator" twice. Two no answers prove she is a truthteller, two yes answers prove she is a liar, and a yes/no or no/yes response means she is an alternator. Can you do it in one question? No, because with only two possible outcomes, you can't classify her amongst three options. You could of course ask a simple question "Are you a woman" twice, and get to the same determination.
Homework:
What is the quickest way to measure 9 minutes with a 4 minute hourglass and a 7 minute hourglass?
References:
536 Puzzles and Curious Problems, Henry Dudeney
Mathematical Circus, Martin Gardner